4.5. Standing Waves

Standing waves are a fascinating interesting of this waves chapter. Standing waves are essentially the physical phenomenon behind why musical instruments exist. When a guitar string is plucked a standing wave is formed as the string vibrates and generates a tone. When a woodwind instrument is blown a standing wave is formed between the ends of the instrument producing the pitch.

To kick off this section I wanted to start with the following use of standing waves in air - levitation. By forming a set of standing waves of air pressure, the scientists are able to levitate small polystyrene beads and manipulate their position in space.

As part of the IB we explore two types of standing waves, as follows:

Forming Standing Waves - What standing waves are and how they form
Standing Waves on Strings - The reason behind why guitars, violins and pianos work
Standing Waves in Pipes - Looking at standing waves in both open and closed tubes

Forming Standing Waves

Let's start with a wave on a string, or through a stretched slinky. When we provide an initial displacement this travels down the length of the string, transferring energy. When this pulse reaches a boundary, it is reflected (with a phase shift of π for a fixed boundary).

If instead of a single pulse, we use a continuous wave, we will instead end up with a superposition of two waves, one incident wave and one reflected wave (the latter of which has been phase shifted by π radians).

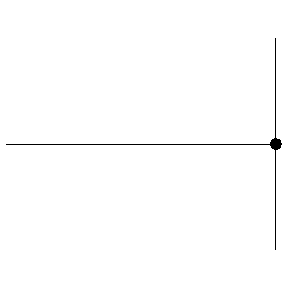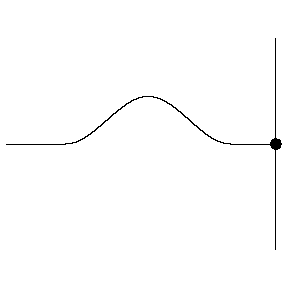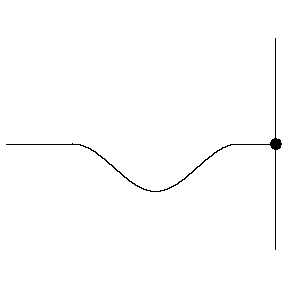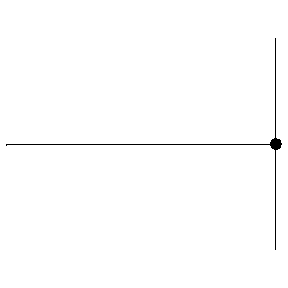
This superposition is shown below. We can see the incident wave travelling to the right, shown in green, with the reflected wave shown in blue. The superposition of these two waves is shown in red and exhibits some interesting behaviour.

The superposition in red below is known as a standing wave.

It contains points of zero displacement, known as nodes, and points of maximum displacement, known as antinodes
There is no net energy transfer overall (energy is transferred equally by the incident and reflected waves).

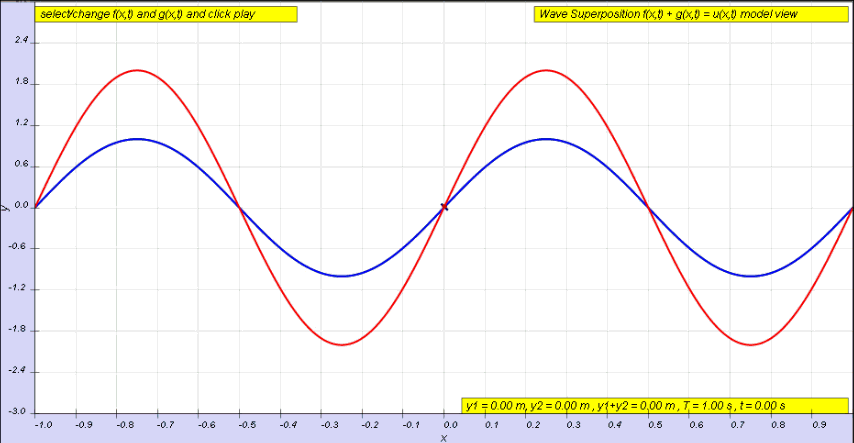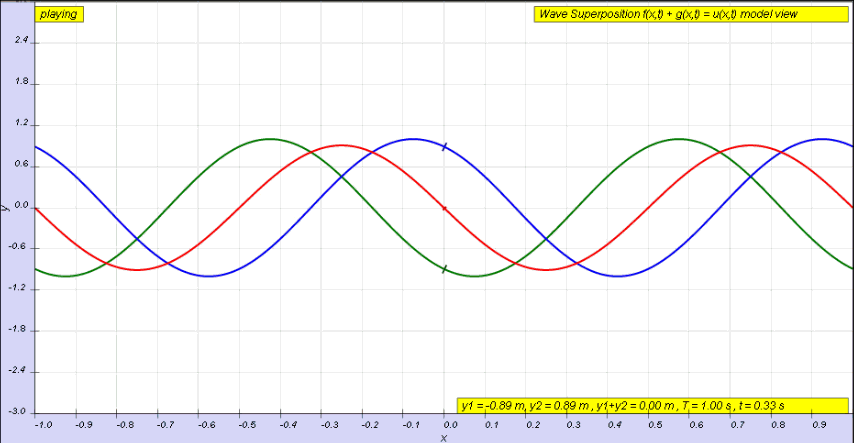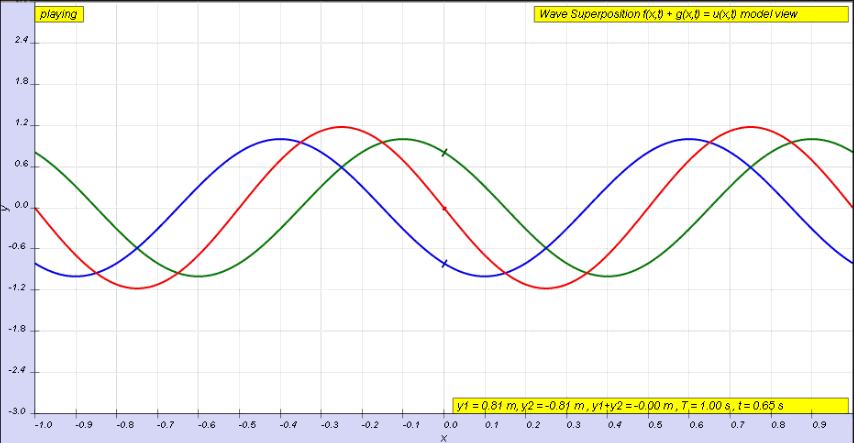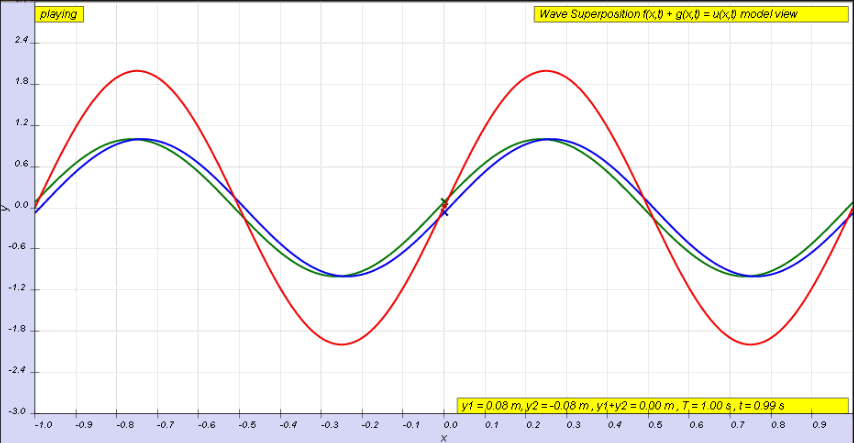
This Walter Fendt simulation is a really clear step-by-step visualisation of a standing wave forming on a string. Observe the formation of nodes and antinodes as the reflected wave progresses.

One key idea to understand is about the phase difference between points on the wave. Geogebra have a simple demonstration of this idea - notice that between nodes, the points are all IN PHASE (i.e. they all reach their maximum displacement at the same time). Two points positioned either side of a node will oscillate IN ANTIPHASE (that is when one reaches its maximum positive displacement, the other will reach its maximum negative displacement.

Most musical instruments function by producing standing waves: whether that is a stringed instrument, a guitar, violin or piano producing a standing wave between the ends of the string; or a wind instrument, such as a clarinet or trumpet producing a standing wave within the column of air inside the intrument.

Standing waves also form on discs and plates - such as with a symbol. When it is struck a series of nodes and antinodes will be formed along the radius of the symbol, producing its pitch. This can be clearly visualised with the Chladni plate - the salt particles get trapped on the nodes, producing a an interesting set of patterns depending on the frequency and geometry.

Standing Waves on Strings

Stringed instruments rely on the formation of standing waves across the ends. A guitar string is fixed at the ends, therefore these ends will always represent nodes. When the string is plucked, the centre of the wave will be an antinode, as it vibrates with maximum displacement.

However, there exist a number of modes of vibration that can be formed, with different number of nodes and antinodes (and different frequencies). These are called the harmonic frequencies. The video below shows the different harmonic frequencies being generated on a vibrating string.

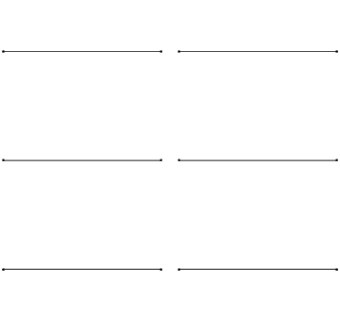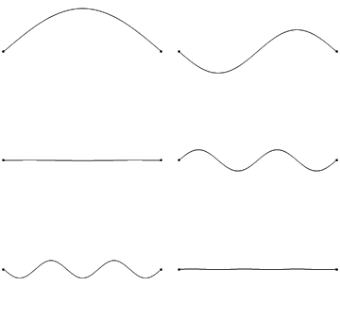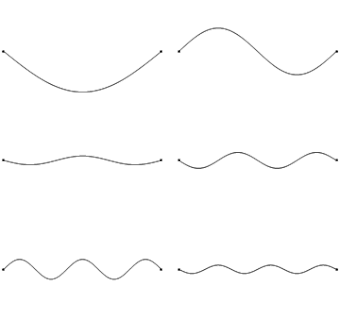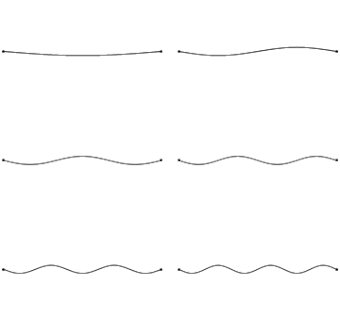
We already know that each end of the string is fixed, therefore must be a node. The simplest harmonic, or fundamental frequency consists of a node on each end, with one antinode in the middle. As we go up through the harmonics, we add a node and antinode each time.

If the string has a length L, we can use our diagrams to work out an expression for our wavelength in terms of L for each scenario (shown in red). Finally, we can use the wave equation (f = v/λ) to work out the frequency of each harmonic (shown in yellow). Compare how the frequency changes as we move up through our harmonic frequencies.

Video Lessons

Chris Doner	Standing Waves and Harmonics		IB Specific
Khan Academy	Standing Waves on Strings
Physics Online	Standing Waves on Strings	Practical Tips
Science Shorts	Standing Waves
Study Nova	Standing Waves

Resources

IB Physics	Topic 4 Notes
IB-Physics.net	Chapter 4 Summary				IB Revision Notes
Isaac Physics	Standing Waves on Strings				Derivation not required
Mr. G	4.5 Teaching Notes	4.5 Student Notes
Physics and Maths Tutor	Waves Definitions	Waves Key Points	Waves Detailed Notes	Waves Progressive & Standing Waves	A Level Resources - content slightly different

Questions

Cambridge University Press	Topic 4: Add Qs	Topic 4: Add Qs MS	Topic 4: MCQs	CUP Website Link	Freely available online
Dr French's Eclecticon	Waves	Waves Solutions		Link to Dr French's Site	Extension: Pre-University Material
Grade Gorilla	4.5 (Standing Waves) MCQ	Topic 4 (Waves B) End Quiz			Quick IB Specific Mixed MCQs
Isaac Physics	Standing Waves				Mixed Questions
Mr. G	4.5 Formative Assessment	Topic 4 Summary Qs			IB Specific Questions
Physics and Maths Tutor	MCQ Progressive/ Stationary (AQA 2)	MCQ Progressive/ Stationary MS (AQA 2)	Superposition & Standing Waves (AQA 2)	Superposition & Standing Waves MS (AQA 2)	A-Level Qs: overlapping content

Standing Waves in Pipes

Wind instruments also make use of resonant frequencies and standing waves. For example, when a trumpet is blown, a standing wave is set up within the tube of the instrument. We can imagine these instruments like a long tube, with an open end at one end, with the other either closed or open.

If the end of the tube is open, the air molecules can vibrate freely, therefore this forms an antinode.
If the end of the tube is closed, the air molecules are unable to vibrate freely, therefore this forms a node.

A demonstration of this idea of resonance is shown in this video below. As the length of the pipe changes, the volume of the sound increases drastically when the harmonic frequency is matched.

This Walter Fendt simulation is my favourite visualisation of standing waves in pipes. It can be quite hard to interpret the longitudinal representation as a transverse wave, so this helps visualise that.

i) Compare the behaviour of the nodes and antinodes as the molecules oscillate back and forth.

ii) Look at what happens as the harmonic changes.

iii) Compare an open ended pipe and a closed ended pipe. How do the positions of the various nodes and antinodes compare?

Standing Wave in an Open Pipe

As stated earlier, an open end corresponds to an antinode, as the air particles there are free to vibrate freely. If each end of the pipe is open, then our simplest frequency corresponds to an antinode at each end, with a node in the middle. Brass instruments (e.g. trumpets) typically follow the physics of open pipes.

The gifs below by ophysics shows the oscillations of air molecules within each of these pipes (along with the transverse representation). A positive displacement means that those particles are to the right of their equilibrium, while a negative displacement means they are to the left.

The left gif shows the fundamental frequency (Antinode-node-antinode), while the right gif shows the second harmonic (A-N-A-N-A). Notice that the nodes vary between being a compression and a rarefaction (you must look at the displacements of the neighbouring particles to work out which it will be)..

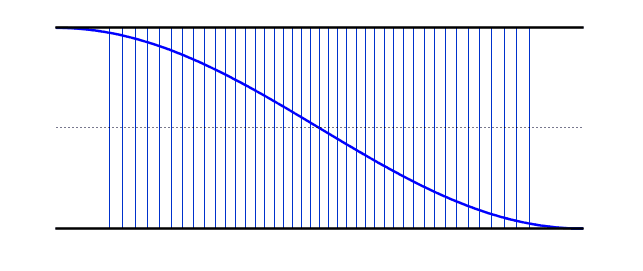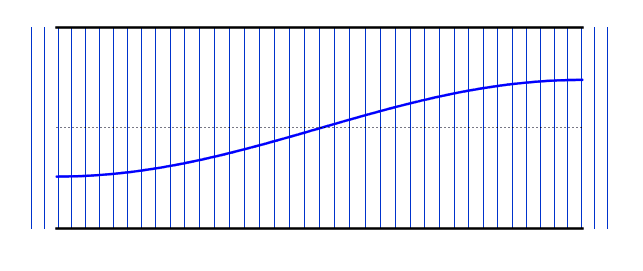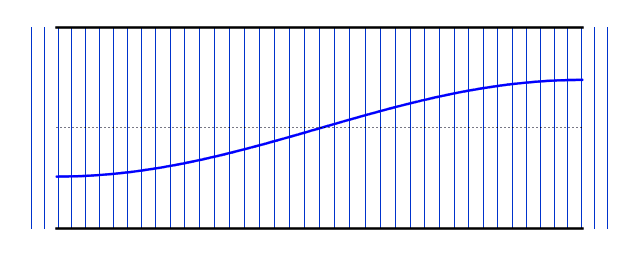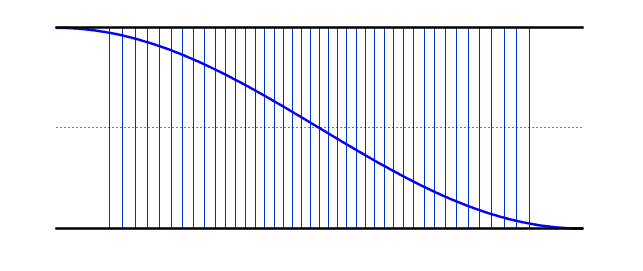
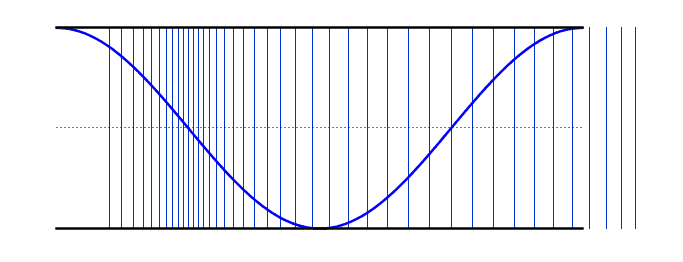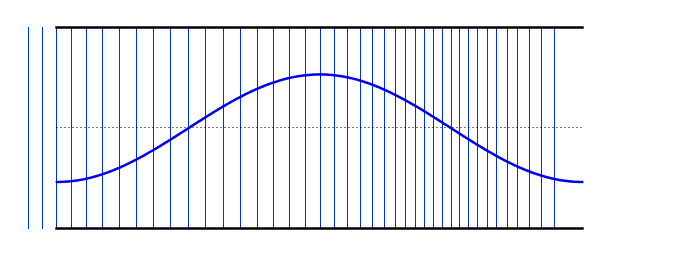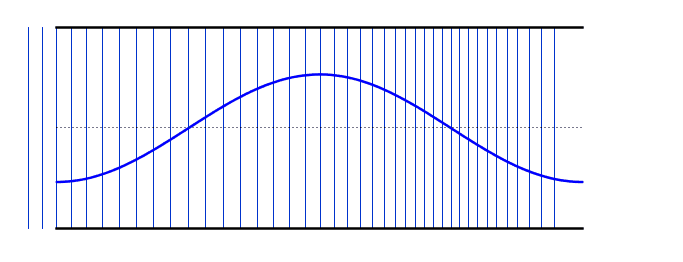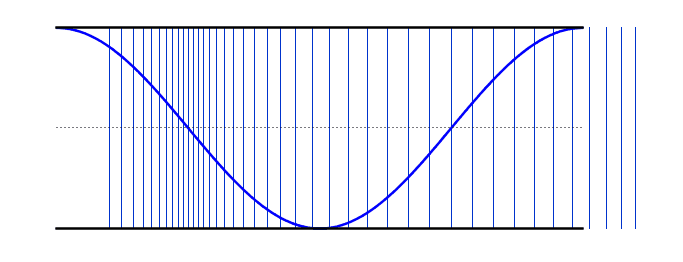
We can use the same logic that we used earlier for the standing waves on strings - i.e. starting with our simplest harmonic frequency and then moving up through our various modes. These differ from the standing waves on the string in that we now have antinodes at each end - however, if you compare the resonant frequency values with the string, you will notice that the behaviour is identical (i.e. 2nd harmonic has double the frequency of the 1st harmonic).

Standing Wave in a Closed Pipe

This time, one end of our pipe is going to be closed. At the closed end, the molecules are constrained by the pipe end, so cannot vibrate freely in that direction. The closed end therefore will be an antinode. Woodwind instruments (e.g. clarinets) typically follow the behaviours of closed pipes (as they use a reed).

The gifs below by ophysics shows the oscillations of air molecules within a closed pipes (along with the transverse representation). In this case our simplest mode of oscillation is simply made up of just a node and an antinode at the closed and open ends respectively.

Now, let's follow the same logic as above, with our new boundary conditions (node on one end, antinode on the other). The harmonic frequencies are shown in yellow. Here, notice that our different resonant modes only produce odd numbered multiples of the fundamental frequency (e.g. f1, 3f1, 5f1...), therefore we only observe the odd numbered harmonics.

Video Lessons

Chris Doner	Standing Waves and Harmonics (Pipes)		IB Specific
Khan Academy	Standing Waves in Open Tubes	Standing Waves in Closed Tubes
Physics Online	Standing Waves in Pipes
Science Shorts	Standing Waves in Pipes
Study Nova	Standing Waves

Resources

IB Physics	Topic 4 Notes
IB-Physics.net	Chapter 4 Summary				IB Revision Notes
Isaac Physics	Standing Waves on Pipes				Derivation not required
Mr. G	4.5 Teaching Notes	4.5 Student Notes
Physics and Maths Tutor	Waves Definitions	Waves Key Points	Waves Detailed Notes	Waves Progressive & Standing Waves	A Level Resources - content slightly different

Questions

Cambridge University Press	Topic 4: Add Qs	Topic 4: Add Qs MS	Topic 4: MCQs	CUP Website Link	Freely available online
Dr French's Eclecticon	Waves	Waves Solutions		Link to Dr French's Site	Extension: Pre-University Material
Grade Gorilla	4.5 (Standing Waves) MCQ	Topic 4 (Waves B) End Quiz			Quick IB Specific Mixed MCQs
Isaac Physics	Standing Waves				Mixed Questions
Mr. G	4.5 Formative Assessment	Topic 4 Summary Qs			IB Specific Questions
Physics and Maths Tutor	MCQ Progressive/ Stationary (AQA 2)	MCQ Progressive/ Stationary MS (AQA 2)	Superposition & Standing Waves (AQA 2)	Superposition & Standing Waves MS (AQA 2)	A-Level Qs: overlapping content

Additional Resources

IB Questions

A question by question breakdown of the IB papers by year is shown below to allow you to filter questions by topic. Hopefully you have access to many of these papers through your school system. If available, there may be some links to online sources of questions, though please be patient if the links are broken! (DrR: If you do find some broken links, please contact me through the site)

Questions on this topic (Section 4) are shown in light blue.

Use this grid to practice past IB questions topic by topic. You can see from the colours how similar the question topic breakdown is year by year. The more you can familiarise yourself with the IB question style the better - eventually you will come to spot those tricks and types of questions that reappear each year.